[文献阅读] A Game-Theoretic Approach to Computation Offloading in Satellite Edge Computing 卫星边缘计算中计算卸载的博弈方法
摘要与主要贡献
- 提出了卫星边缘计算中计算卸载策略优化的博弈论方法,建立了一个计算卸载博弈框架,并基于排队论计算了任务的响应时间和能量消耗,作为优化性能的度量。提出了一种迭代算法来搜索博弈的纳什平衡。表明基于游戏的卸载策略可以大大降低设备的平均成本。
- 考虑到卫星引起的间歇性通信,只有在窗口期才能够进行通信,并假设卫星上只部署一个MEC服务器
- KPI:响应时延与能耗
系统模型
应用场景
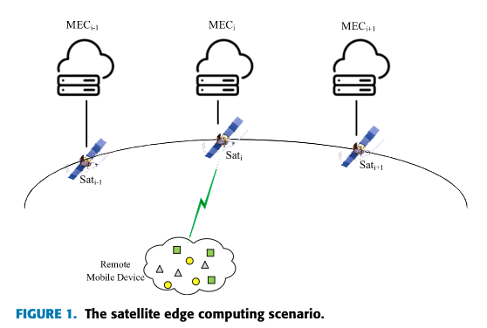
轨道模型
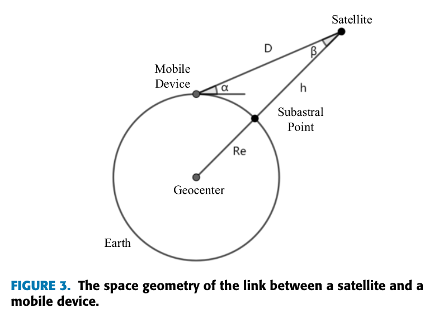
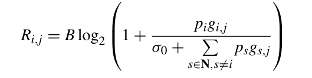 >定义一个(轨道)周期内的通信时间
>𝜃={𝜃1,𝜃2,...𝜃𝑀},0≤𝜃𝑗≤1
>𝜃𝑗表示设备在轨道周期内可以与卫星j通信的时间的百分比。
>定义一个(轨道)周期内的通信时间
>𝜃={𝜃1,𝜃2,...𝜃𝑀},0≤𝜃𝑗≤1
>𝜃𝑗表示设备在轨道周期内可以与卫星j通信的时间的百分比。
通信模型
移动设备i到卫星j的上行链路数据速率𝑅𝑖,𝑗 B表示信道带宽,Pi表示设备i的发射功率,𝑔𝑖,𝑗表示设备i与卫星j之间的信道增益,σ0表示背景噪声功率
- 只考虑上传时间,忽略返回结果的下载时间(结果数据远远小于上传数据)
可以得知 * 任务的传输速率𝑅𝑖,𝑗与设备的发射功率𝑃𝑖成正相关 * 过高的发射功率𝑃𝑖会导致过多的能量消耗 * 过多设备的卸载,将导致速率降低
计算模型
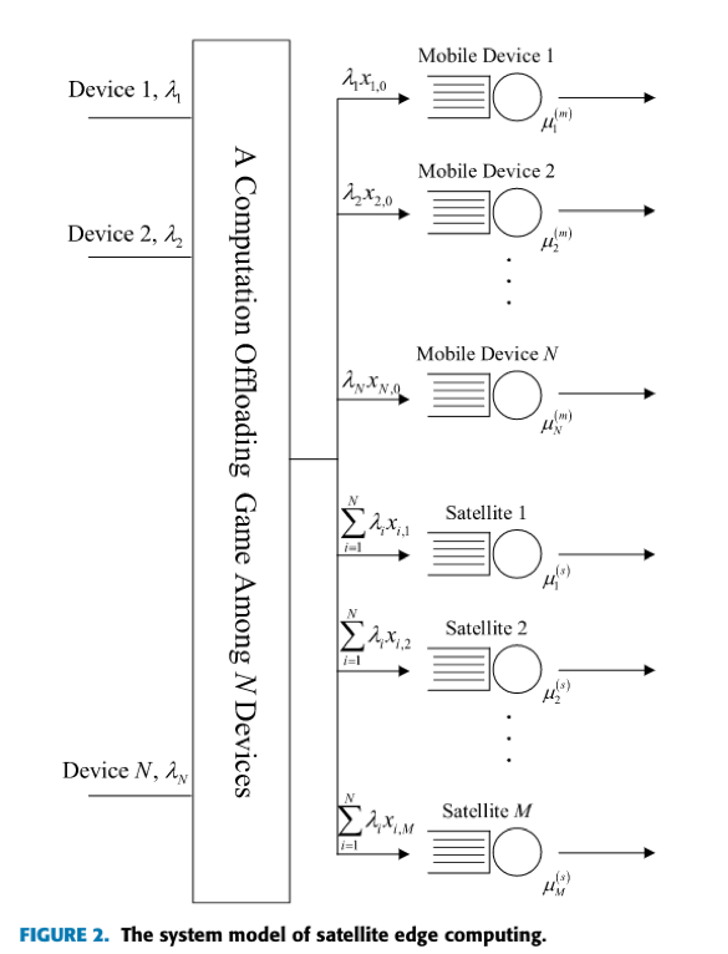
假设每个移动设备可以生成一系列同类任务。 设备i生成的任务可以用所需的资源和数据大小来表示,即 Taski = {ci,di},$𝐶_{(𝑚)}^{𝑖}$和$𝐶_{(𝑠)}^{𝑗}$是设备和卫星的计算能力,为随机变量,用一秒CPU周期数表示 。 均值表示为$\bar{(𝑐_𝑖)}$,$\bar{(𝑑_𝑖)}$,二阶矩为$\bar{(c_𝑖^2)}$ 和$\bar{(d_𝑖^2 )}$ 设备i在本地执行并和分流到卫星的任务的百分比定义为设备i的计算分流策略 𝐱𝑖={𝑥𝑖,0,𝑥𝑖,1...𝑥𝑖,𝑀}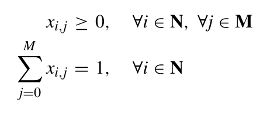
约束条件 * 百分比大于0(0表示不往该设备卸载) * 所有的百分比相加为1 * 隐含:每个都要小于1
博弈论模型
令𝑋=𝑋1∗𝑋2∗...𝑋𝑁是所有设备策略组合的集合,所有设备的整体策略我们可以用𝐱={𝐱1,𝐱2,…,𝐱𝑁} 表示,中间的𝐱𝐢表示设备i的策略 $𝐱_{−𝐢}=({𝐱_{1},...𝐱_{𝑖−1},𝐱_{𝑖+1}…,𝐱_{𝑁}})∈𝑋$表示除玩家𝑖以外的所有玩家策略的向量 KPI(性能指标)选择平均响应时间和平均功耗作为性能指标,成本函数计算如下 $P_{𝑖}(𝑥_{𝑖}, 𝑥_{(−𝑖)}) = 𝑇_{𝑖} + 𝜇_{𝑖}𝐸_{𝑖}$

计算任务卸载到卫星
卸载的平均响应时间
计算任务从移动设备i分流到卫星j,需要执行三个步骤:卸载任务,在卫星上执行,返回结果 由于卫星的高动态性,i不能总是和j通信,因此需要考虑通信的等待时间 卸载的平均响应时间 > 个人思考:要是卫星刚好快离开通信区域时任务才卸载,那等结果返回时应该是要加上一个卫星的周期,此公式并不严谨
卫星轨道引起的等待时间与设备i到卫星j通信的时间百分比有关,通信百分比为𝜃𝑗,卸载平均等待时间和平均等待结果返回时间为
> 个人思考:要是卫星刚好快离开通信区域时任务才卸载,那等结果返回时应该是要加上一个卫星的周期,此公式并不严谨
卫星轨道引起的等待时间与设备i到卫星j通信的时间百分比有关,通信百分比为𝜃𝑗,卸载平均等待时间和平均等待结果返回时间为
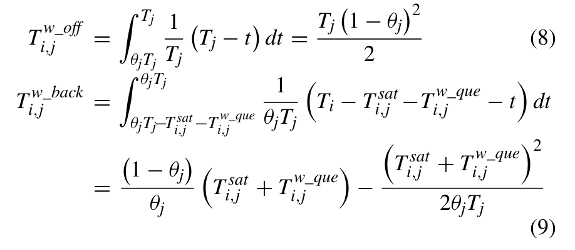 $𝑇𝑗≫T_(𝑖,𝑗)^sat+ T_(𝑖,𝑗)^{(𝑤𝑞𝑢𝑒)}$, 𝑇𝑗是卫星j的轨道周期
$𝑇𝑗≫T_(𝑖,𝑗)^sat+ T_(𝑖,𝑗)^{(𝑤𝑞𝑢𝑒)}$, 𝑇𝑗是卫星j的轨道周期
个人思考:不是很明白这两个公式的含义,如果算平均时间,根据均值定理(8)公式分母应该是上标-下标,(9)公式同理根据M/G/1排队理论,卫星j上任务的平均排队等待时间为
 >采用M/G/1排队模型,使用p-k公式计算平均等待时间
总式子
>采用M/G/1排队模型,使用p-k公式计算平均等待时间
总式子
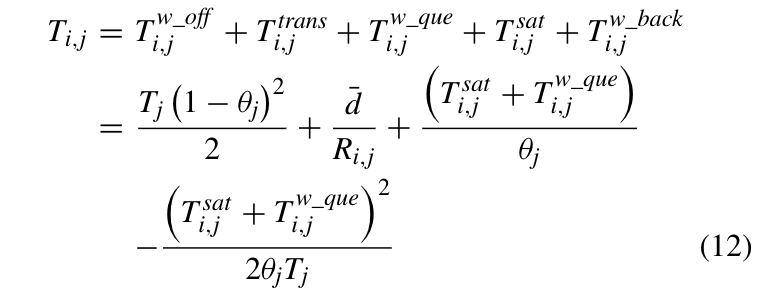 ### 卸载到卫星的能耗
由$E_{(𝑖,𝑗)}^{𝑡𝑟𝑎𝑛𝑠}$平均传输消耗, $E_{(𝑖,𝑗)}^{sat}$平均处理消耗
$𝑃_{𝑖}$为i的传输消耗
由于CPU的能耗与CPU的频率的平方成正比,得
其中κ是取决于芯片架构的有效开关电容
总式子
### 卸载到卫星的能耗
由$E_{(𝑖,𝑗)}^{𝑡𝑟𝑎𝑛𝑠}$平均传输消耗, $E_{(𝑖,𝑗)}^{sat}$平均处理消耗
$𝑃_{𝑖}$为i的传输消耗
由于CPU的能耗与CPU的频率的平方成正比,得
其中κ是取决于芯片架构的有效开关电容
总式子
分流到本地执行
同样采用M/G/1排队模型 执行任务的平均响应时间$𝑇_{(𝑖,0)}$ = 在i上的平均等待时间$T_{(𝑖,0)}^{(𝑤𝑞𝑢𝑒)}$ + 平均执行时间$T_{(𝑖,0)}^{loc}$ 执行时延 本地排队时延 本地排队时延 能耗 其中κ是取决于芯片架构的有效开关电容总式子
时延
能耗
纳什均衡的证明和唯一性证明
在博弈中,如果每个参与者在已知其他参与者的策略下,采用最优策略来应付,那么我们就达到了一个纳什均衡,同时也意味着没有人能通过改变自己的策略,获得更好的结果。占优策略 * 在选择策略时,有一个策略的效用总是大于其他所有策略的效用时,我们把这类策略称为占优策略。 占优策略纳什均衡 * 当所有参与者的最优回应时选择他们的占优策略时,这时达到的纳什均衡称为占优策略。定理1
非合作博弈,至少存在一个纳什均衡 * 条件1:策略空间$𝑋_{𝑖}$是欧几里得空间的非空,凸且紧凑的子集 * 条件2:成本函数$P_{𝑖}$($𝑥_{𝑖}$, $𝑥_{−𝑖}$)连续且在$𝑋_{𝑖}$为凸定理2
一个连续的二次可微函数P(x),其中x = (x1, x2,…xM)当且仅当其二阶偏导数的Hessian矩阵为正定时,为凸。黑塞矩阵 计算 为正定矩阵,根据定理2位凸 根据式子
证明其是占优可解且纳什均衡唯一
算法

初始分布为$𝑥_{𝑖}= (1/(M+1), 1/(M+1), …, 1/(M+1))$
在每次迭代中,每个设备都会搜索当前情况下的最优卸载策略$𝑥_{𝑖}^{,}$,和计算最小代价函数$P_𝑖(𝑥_𝑖^,)$ 。𝜀 代表精度需求
$𝑥_{𝑖}^{,}$,用拉格朗日法求解梯度,例如
每次迭代寻找最优的$𝑥_{𝑖}^{,}$
根据纳什均衡的特点,只有当成本函数减少时,策略才会更新。当两个策略足够接近时,算法终止。
最后的收敛策略$𝑋^∗$是任务卸载游戏的纳什均衡。
实验仿真
论文中实验仿真对比的算法为全本地卸载,随机卸载,平均卸载,对比的算法均为最简单的卸载算法,意义不大
具体实验仿真参考论文